Career History

Positions Held

  • 2021–Present: Lecturer (University of Bath)
  • 2017–2021: Teaching Fellow (University of Bath)
  • 2016–2017: Associate Lecturer (Cardiff University)
  • 2011–2017: Teaching Assistant (Cardiff University)

Educational History

The development of disturbances in plane channel flow between compliant walls is studied. It is well known that compliant walls have the ability to stabilise the Tollmien-Schlichting instability arising from the flow. However, given the wave-bearing nature of compliant walls, wall-based instabilities can be generated. In the absence of any modal interactions, the predominant wall-based instabilities are those known as divergence and travelling wave flutter which have their origins in the free-waves that can propagate in either direction along a compliant wall in the absence of any fluid.

The treatment of the problem at hand is mainly numerical, in particular two numerical approaches are used. The first involves solving the coupled fluid flow/compliant wall system of stability equations for disturbances with a normal mode form and the second is through direct numerical simulations for a finite compliant wall.

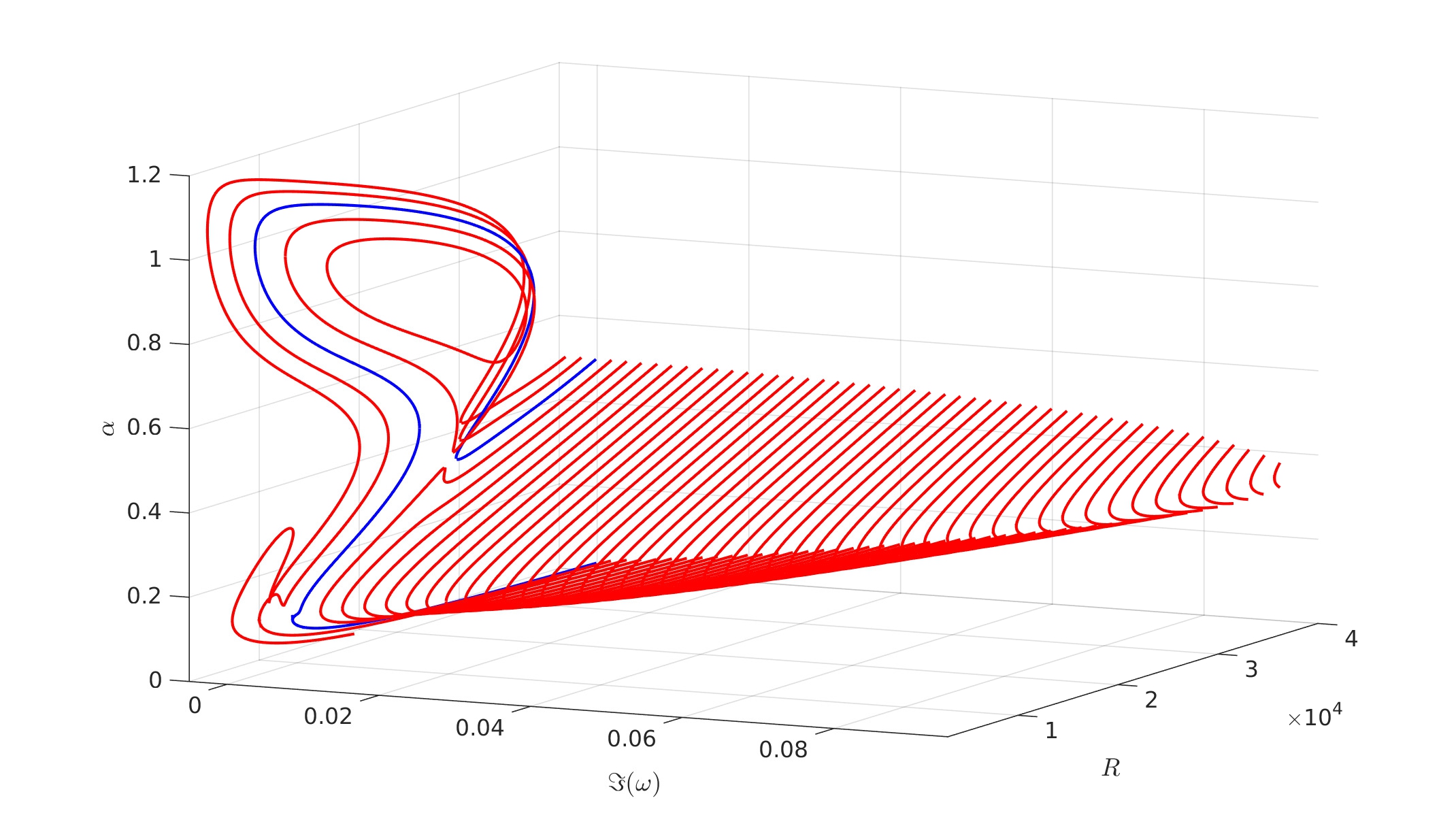
The results presented here show that the normal mode solutions of the governing equations can provide excellent predictions for the wavenumbers that characterise the compliant wall displacements for the wall-based modes that arise in the simulations. This documents the onset of the wall-based instabilities using the current simulation method and this has not been systematically studied before. Additionally, and perhaps most interestingly, they can also predict some aspects of the contribution from end effects for finite wall simulations even though the numerical procedure used to obtain said solutions has been designed for an infinite compliant wall.

Finally, cases which display different types of instability in action and the range of possibilities for the spatial and temporal evolution are presented. Modal interactions between wall-based modes and those that can persist in a rigid channel are discussed and used to analyse the onset of global and absolute instability. These instabilities are studied from three different points of view: normal mode solutions of the fluid flow/compliant wall system, two-dimensional global mode computations and the direct numerical simulations.

  • 2008–2012, Cardiff University: MMath, dissertation on The Rotation Number Of Schrödinger Equations With Periodic And Limit-Periodic Potentials, supervised by Professor Karl M Schmidt.

Awards

Univerity of Bath

  • Outstanding Contribution to Peer Support, 2025
  • Mary Tasker Award, 2025
  • Best Overall Lecturer in the Department of Mathematical Sciences, 2022
  • Best Lecturer of an Applied Module in the Department of Mathematical Sciences, 2022
  • Best Unit (Ordinary Differential Equations & Control Theory) in the Department of Mathematical Sciences, 2022

Cardiff Univeristy

  • Most Influential Member of Staff in the Final Year, 2015
  • Enriching Student Life Award - Most Uplifting Staff Member, 2015
  • EPSRC Postgraduate Studentship, 2012
  • IMA Award for High Undergraduate Achievement, 2012