Appendix A — MATLAB Basics

This Appendix will cover some of the basic procedures in MATLAB.

A.1 Command Window

When MATLAB is opened, you will be faced with a window containing several parts.

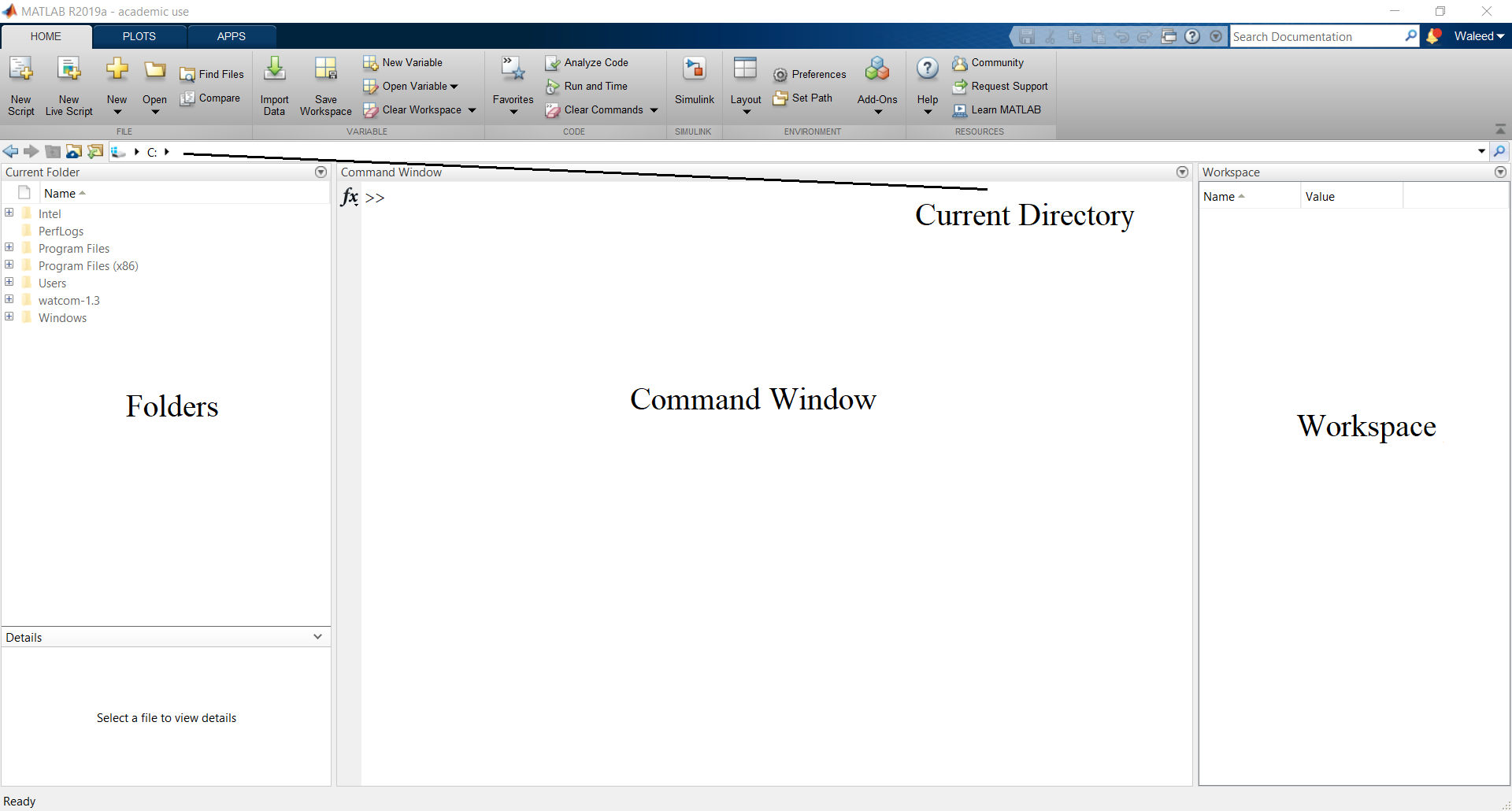
These different areas serve the following purpose:

Command Window: This is the main window where the first line starts with >>. This is where commands are executed, note that once a command has been run (i.e. you pressed Enter), then what has been written cannot be edited or undone and therefore, this is a suitable space for running or executing codes only, not for writing extensive codes.
Directory: This is the destination folder that MATLAB is going to refer to in either opening or saving codes. Note that all MATLAB files are saved as .m files.
Current Folder: This displays the functions, figures, subfolders, scripts, codes, etc. that are in the current directory.
Workspace: This displays all the the variables that have been used, along with their types (number, matrix, etc.) and their values.

A.2 Executing Commands in the Command Window

The command window will be where all the codes and functions are executed. It can also be used to perform quick calculations. Some examples of MATLAB syntax and built-in functions are shown below:

Mathematical Symbol	MATLAB Syntax
$+$	`+`
$-$	`-`
$\times$	`*`
$\div$	`/`
$3^5$	`3^5`
$\pi$	`pi`
$\mathrm{e}^2$	`exp(2)`
$\sin(\pi)$	`sin(pi)`
$\sin^{-1}(\pi)$	`asin(pi)`
$\lfloor 3.6 \rfloor$	`floor(3.6)`
$\lceil 4.7 \rceil$	`ceil(4.7)`
$\left\| -4 \right\|$	`abs(-4)`
$1+2\mathrm{i}$	`1+2i`
$\mathrm{i}$	`0+i`
$\Re(1+2\mathrm{i})$	`real(1+2i)`
$\Im(3-4\mathrm{i})$	`imag(3-4i)`
$2 \times 10^7$	`2e7`
$147 \; (\mathrm{mod} \; 5)$	`mod(147,5)`

All trigonometric functions follow the same syntax as sin, but bear in mind that by default, all the angles should be in radians and not in degrees. To use degrees, just put a d at the end of the trigonometric function, i.e. use sind, cosd, asind, etc.

The functions $\lceil \bullet \rceil$ and $\lfloor \bullet \rfloor$ are the ceiling and floor functions respectively. Their purpose is to round up to the nearest integer (ceiling) or round down to the nearest integer (floor). Standard rounding can be done using round.

Another important function is mod which find the remainder when dividing one number by another. For example, $147 \; (\mathrm{mod} \; 5)$ is the remainder after dividing $147$ by $5$ which is $2$.

>> 2+2
ans =
     4
>> sin(0)
ans =
     0
>> sin(pi/2)
ans =
     1
>> sin(30)
ans =
     -0.9880
>> sind(30)
ans =
     0.5000
>> pi
ans =
     3.1416
>> exp(1)
ans =
     2.7813
>> ceil(2.1)
ans =
     3
>> floor(6.9)
ans =
     6
>> round(2.3)
ans =
     2
>> mod(147,5)
ans =
     2

If the outcome of a calculation is an integer, then MATLAB will usually display it as an integer, if not, then by default, it will display the solution as a number to 4 decimal places. The number of decimal places can be increased by using format long and reversed by using format short.

Note

Note that any command executed in the Command Window will be applied globally, so if format long is used, it will apply to everything executed in the Command Window until it is reversed or MATLAB is restarted.

>> pi/2
ans =
     1.5708
>> format long
>>pi/2
ans =
     1.570796326794897
>> format short
>> pi/2
ans =
     1.5708

A.3 Defining Variables

MATLAB is a numerical programming language that relies on a “box” feature. This means that standard algebraic practices cannot be used, for instance, writing $2x=x+1$ makes perfect sense mathematically and yields a solution of $x=1$, however writing 2*x=x+1 makes no sense in MATLAB.

Note

A very important note to bear in mind here is that in MATLAB syntax, 2x has no meaning. In order to multiply terms, the multiplication sign * needs to be used.

A “box” with a given name, which is always on the left hand side of the = sign, is assigned a value, which is on the right hand side, and the value can then be manipulated or changed, so there are no variables in MATLAB per se. In the following example, a “box” is given the name x and the number 3 is assigned to it, calculations can then be done by referring to the number that is in said box. The values within the boxes can be redefined by using the = sign again.

>> x=3
x =
     3
>> x+1
ans =
     4
>> x+x
ans =
     6
>> 3*x
ans =
     9
>> y=(2*x)^x
y =
     216
>> y+10
ans =
     226

On the other hand, $x=x+2$ makes no sense mathematically but within MATLAB syntax (as is the case with most other programming languages), this simply means calculate x+2 (which is on the right hand side of the = sign) using the value already in the box labelled x (which is 3), then redefine the value in that same box to take this new value, so the box labelled x is now assigned the value 5.

>> x=3
x =
      3
>> x=x+2
x =
      5
>> x=3*x
x =
      15

A.4 Naming Variables

There are certain rules with regards to what names can be used for the variables:

Names can be of any length (within the bounds of reason of course to avoid confusion).
Names are case sensitive, so a and A are two different variable names.
Names must contain no spaces, underscores can be used instead. For example, Bad Name is not a viable variable name but GoodName and Also_A_Good_Name are both valid.
Names must contain no operators or symbols, with the exception of the underscore, so do not use ! ? . , ; + - * / & # % $.
Names can contain numbers as long as they are not the first character. For example 1Forrest1 is not a viable variable name but OneForrest1 or Obi1Kenobi are both viable.
Names cannot be the same as already existing functions, for instance, a variable cannot be given the name sin since there is already a built-in function with that same name, however, one could use Sin since variable names are case sensitive (although this particular example is not recommended since it may cause confusion).

>> P_1=1
P_1 =
     1
>> P_2=P_1+2
P_2 =
     3
>> PP_3=P_1+p_2
Undefined function or variable 'p_2'.
>> PP_3=P_1+P_2
PP_3 =
     4

Typing whos x in the command window will give the properties of x, namely its size (in a matrix sense), storage allocation, class and attributes, but not its value. Typing whos on its own will give a list of all the variables that have been used along with their properties, alternatively, these can also be found in the Workspace.

A.5 Scripts & Functions

Within the command window, nothing can be edited once it has been executed which is inconvenient if the code is longer than a single line. In that case, it is best to use the Editor. By default, the Editor can be opened by clicking on New Script, this is a window in which any length of code can be written, saved and then executed with the Run button. If any changes need to be made then the editor window will allow that with ease, once changes are made, the code can be run again.

A function is very similar to a script but the difference between them is that a function can take in several inputs and produce several outputs and must always have the format:

function [output1,output2,...]=Function_Name(input1,input2,...)
    Body of the code
end

The function cannot always be executed with the Run button but will often need to be called in the Command Window to allow for the inputs to be placed.

The name of the function follows the same rules as the variable names mentioned before. One of the most important technicalities that has to be addressed is that the functions and scripts that are used must be in the same as folder as is stated in the directory.

When writing functions, or scripts of any kind, there are two important characteristics that need to be considered:

Commentary: When writing codes, it is important to provide some comments on what is being done to give context and to allow for accessibility and reproducibility. This can be done by using % at the beginning of the line. This makes MATLAB ignore everything that comes after it, allowing for commentary of bits of code that need context. This is generally good practice in writing codes since the user can make comments about inputs, outputs, procedures, etc. without affecting the execution of the code.
Suppression: On MATLAB, any line of code that is written will produce an output (many other coding languages do not unless prompted to do so). So in functions, performing an action will always produce an output whether it is needed or not. This is where semicolon ; can be used. The semi-colon suppresses the output, this means that if there are several calculations to be made, sometimes the intermediate stages do not need to be seen, only the final answer, in this case the semicolon allows the calculation to be done but not printed out in the command window.

Example of function

Consider a cube with side length $L$ (in m) and mass $M$ (in kg), then the object will have density \[\rho=\frac{M}{L^3}.\] The following code calculates this density with the inputs being the mass $M$ and length $L$ with the output being the density $rho$:

function [rho]=Calculate_Density(M,L)

% M:  Mass of cube in kg
% L:  Side length of cube in m

rho = M/(L^3);

end

This function, which is called Calculate_Density, has two inputs, namely M and L, and one output, namely rho. Notice that the list of inputs must always be in round brackets (...) while the outputs should be in square brackets [...].

To use this function, just type the name of the function in the command window with the inputs and outputs in exactly the same order in which they appear in the function and using the same set of brackets as well, i.e. (...) for inputs and [...] for outputs.

>> [rho] = Calculate_Density(100,20)
rho =
     0.0125

Expanding on this, suppose that a new function is desired where the user will input the mass in pounds and the length in inches but the desired density should still be in $\mathrm{kg \; m}^{-2}$. A few more lines can be added in that case.

function [rho]=Calculate_Density_Imperial(M,L)

% M:  Mass of cube in lbs
% L:  Side length of cube in inches

M = M/2.20462;     % Converts lbs to kg
L = L/39.3701;      % Converts inches to m

rho = M/(L^3);

end

Note that here, the same variable name has been used and then redefined. So initially, M will be input in pounds, say M=50, then at line 6, the same variable name is redefined, so the new mass will be $M=\frac{50}{2.20462}=22.6796$, but the same name is used for both. Similarly for L when it is converted from inches to meters.

In this case, the function can be executed with a mass of 50lbs and a side length of 10in to give:

>> [rho] = Calculate_Density_Imperial(50,10)
rho =
     1.3840e+03

One of the major differences in using scripts and functions is the assignment of variables and their declaration. In a script, if a variable $C$ was given the value 3 (so C=3 was in the script) then this value of $C$ will be declared globally, meaning that it can be used in the command window and it will still take the same value. However in functions, the variables are declared locally, so if in a function the variable $C$ was given the value 3, this will only hold within the function itself and no where outside it.

A.6 Exersises

Excersise 1: Metric Cone

Write a MATLAB function that takes inputs $h$ and $r$ and outputs the volume of a cone (in cubic meters) with height $h$ in meters and radius $r$ in meters.

Test the code on a cone with height 5m, radius 3m (which should give a volume of 47.1238898$\mathrm{m}^3$.

Solution 1

function [V]=Cone_Vol1(h,r)

% This function caculates the volume of a cone in m^3

% Inputs:
% h:  Height of the cone in m
% r:  Radius of the cone in m

% Output:
% V:  Volume of the cone in m^3

V=pi*(r^2)*h/3;

end

Code test with $h=5$ and $r=3$:

>> [V]=Cone_Vol1(5,3)
V =
     47.129

Excersise 2: Imperial Cone

Write a MATLAB function that takes inputs $h$ and $r$ and outputs the volume of a cone (in cubic meters) with height $h$ in inches and diameter $d$ in yards.

Test the code on a cone with height 10in, diameter 1yd (which should give a volume of 0.0556$\mathrm{m}^3$.

Solution 2

function [V]=Cone_Vol2(h,d)

% This function caculates the volume of a cone in m^3

% Inputs:
% h:  Height of the cone in inches
% d:  Diamater of the cone in yards

% Convert h from inches to metres
h = h*0.0254;

% Convert d from yards to metres
d = d*0.9144;

% Radius of cone base is half the diameter
r = d/2;

% Output:
% V:  Volume of the cone in m^3

V=pi*(r^2)*h/3;

end

Code test with $h=10$ and $d=1$:

>> [V]=Cone_Vol2(10,1)
V =
     0.0556